Now entering
The Office
This is my public repository where I store my personal collection of knowledge that I am eager to share.
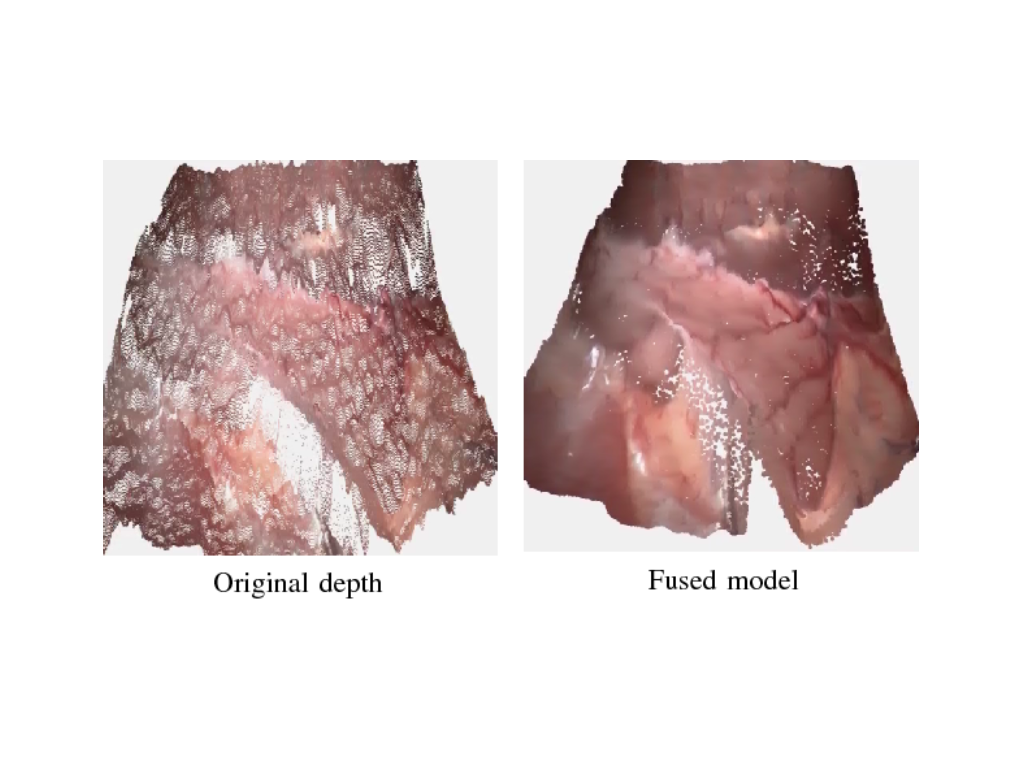
MIS-SLAM
MIS-SLAM: minimum invasive surgery SLAM system offers major improvements: (J. Song, 2018) proposed a heterogeneous architecture that maximises the utilisation of both GPU (dense deformable SLAM) and CPU (ORB-SLAM) to recover the densely deformed 3D structure of the soft tissues in an MIS situation. CPU computational capability is completely used to perform an enhanced ORB-SLAM that provides GPU modules with complementing information. GPU and CPU modules are extensively integrated to increase performance and efficiency
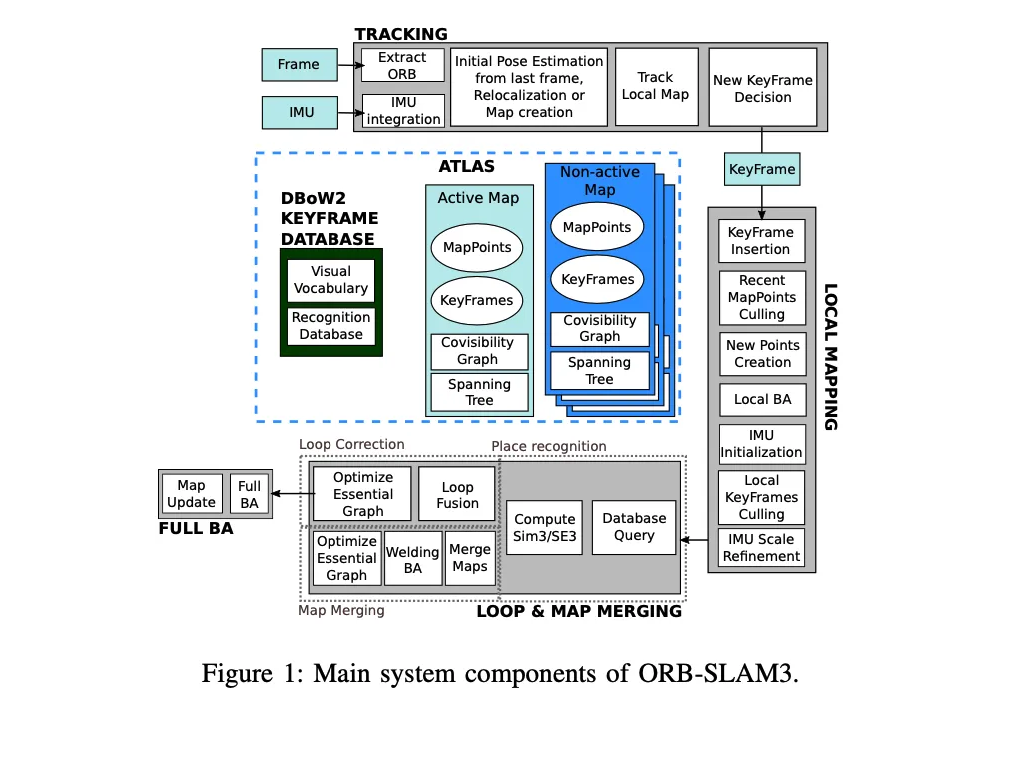
ORB-SLAM3
ORB-SLAM3: Oriented FAST (Features from accelerated segment test) and Rotated BRIEF (Binary Robust Independent Elementary Features) SLAM system is an open-source SLAM library with a fast and accurate IMU initialisation technique using the pin-hole and fish-eye camera (C. Campos R. E.). The ORB-SLAM3 system is an enhanced version of the previous ORB-SLAM, and it can exploit short-term, mid-term, long-term, and multi-map data associations with more precision than any other system.
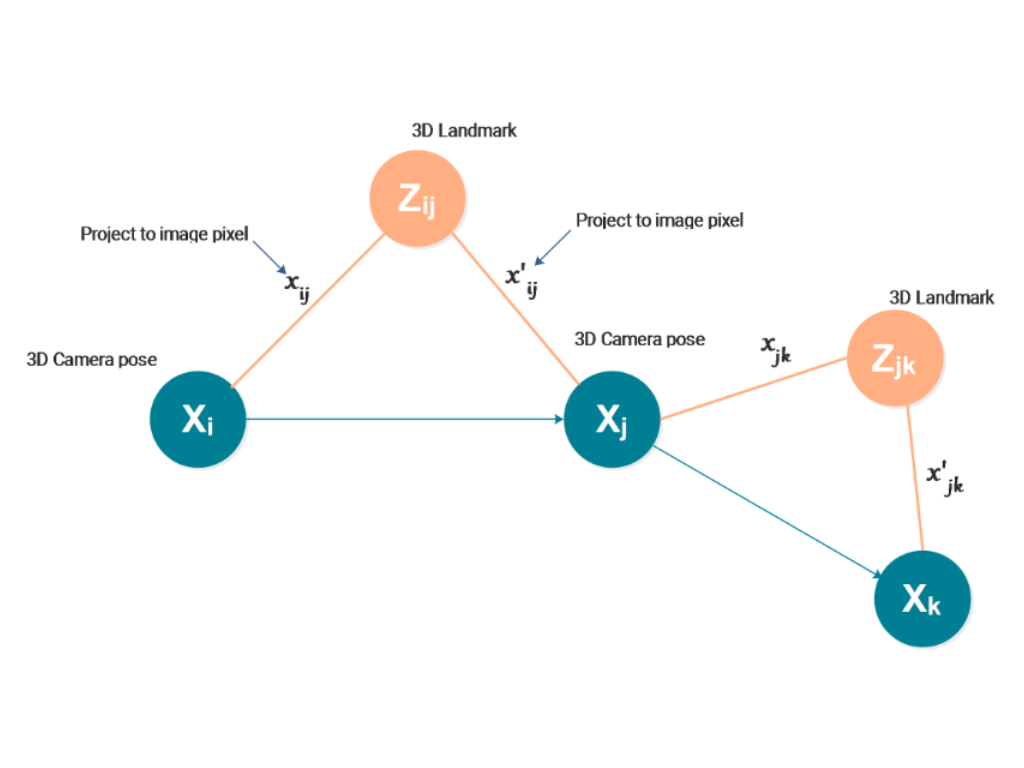
SLAM and Pose Graph Optimisation
Pose Graph Optimisation is a key component of SLAM algorithms that aims to improve the robot's trajectory estimation by minimising the difference between observed and predicted sensor measurements. This is accomplished by constructing a graph that represents the robot's trajectory, with each node representing a pose estimate at a specific time and each edge representing the relationship between adjacent poses. The algorithm can improve the accuracy of the robot's trajectory estimate and the map of the environment by optimising the graph.

Least Squares for Graph-Based SLAM
Graph-Based SLAM (Simultaneous Localisation and Mapping) represents spatial relationships in an environment through the use of a graph. Each node in the graph represents a robot pose or landmark, and each edge represents a spatial constraint from sensor observations. The technique of Least Squares is utilised to minimise the sum of squared differences between these observed and expected values. The objective is to identify the node configuration (i.e., the most likely map and trajectory) that minimises the overall disparity. This method offers a practical approach to managing uncertainty in robotic mapping and localisation tasks.
